Automated essay scoring (AES), where a computer algorithm scores student essays automatically, is an important application of natural language processing for education and language learning.
Traditionally, AES has been solved by non-neural machine learning models such as multivariate regression with handcrafted features. Use of pretrained language models such as BERT (Devlin et al. 2018) has only recently caught on, and its result is still mixed.
In this article we'll review some of the recent advances in automated essay scoring. See (Ke and Ng 2019) for a very good review of traditional and neural, pre-BERT AES methods.
Pre-BERT Neural Models
Two early pioneering works in the use of neural networks for AES are (Taghipour and Ng 2016) and (Alikaniotis et al. 2016).
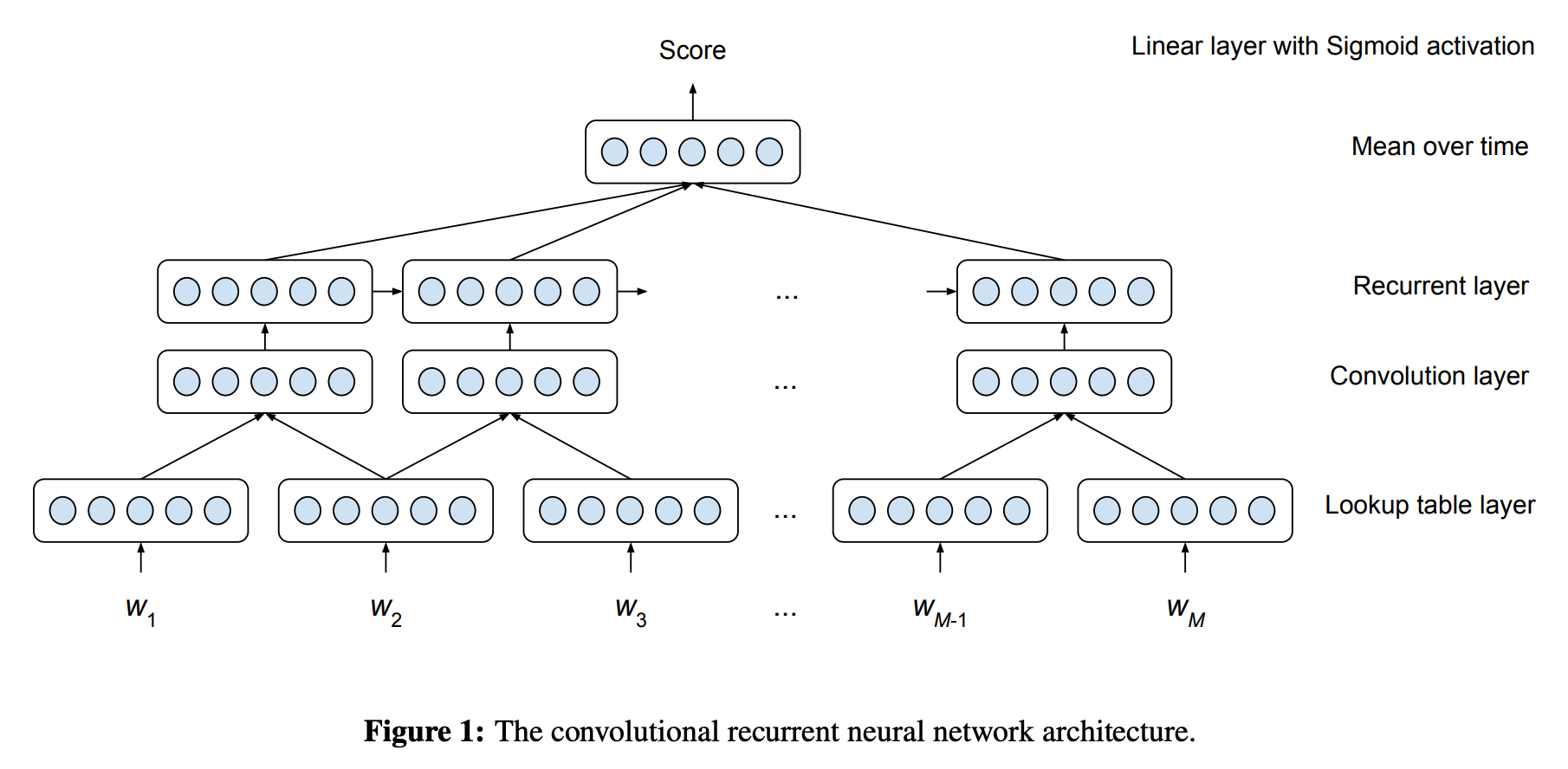
Taghipour and Ng applied a neural network that consists of an embedding lookup layer, a convolution layer, and an RNN (LSTM). The hidden states from the RNN are then averaged over, which are then fed to a linear layer followed by a sigmoid activation (see the figure above). The final prediction is a normalized score between 0 and 1.
One thing to note is the use of the averaged hidden states (called mean over time, or MoT) is very common in AES, while in many other NLP applications, the hidden states of the final RNN cell (or concatenation of the first and the last, if the RNN is bidirectional) are often used. The authors note that MoT was more effective than to use just the last states.
They tested their model on the ASAP Kaggle dataset, a standard AES dataset used in numerous studies. Their model outperforms baselines with traditional, hand-crafted features and regression models (support vector regression and Bayesian linear ridge regression).
Alikaniotis et al. 2016, a concurrent work to Taghipour and Ng above, use a two-stage strategy to train a neural network that can score essays automatically.
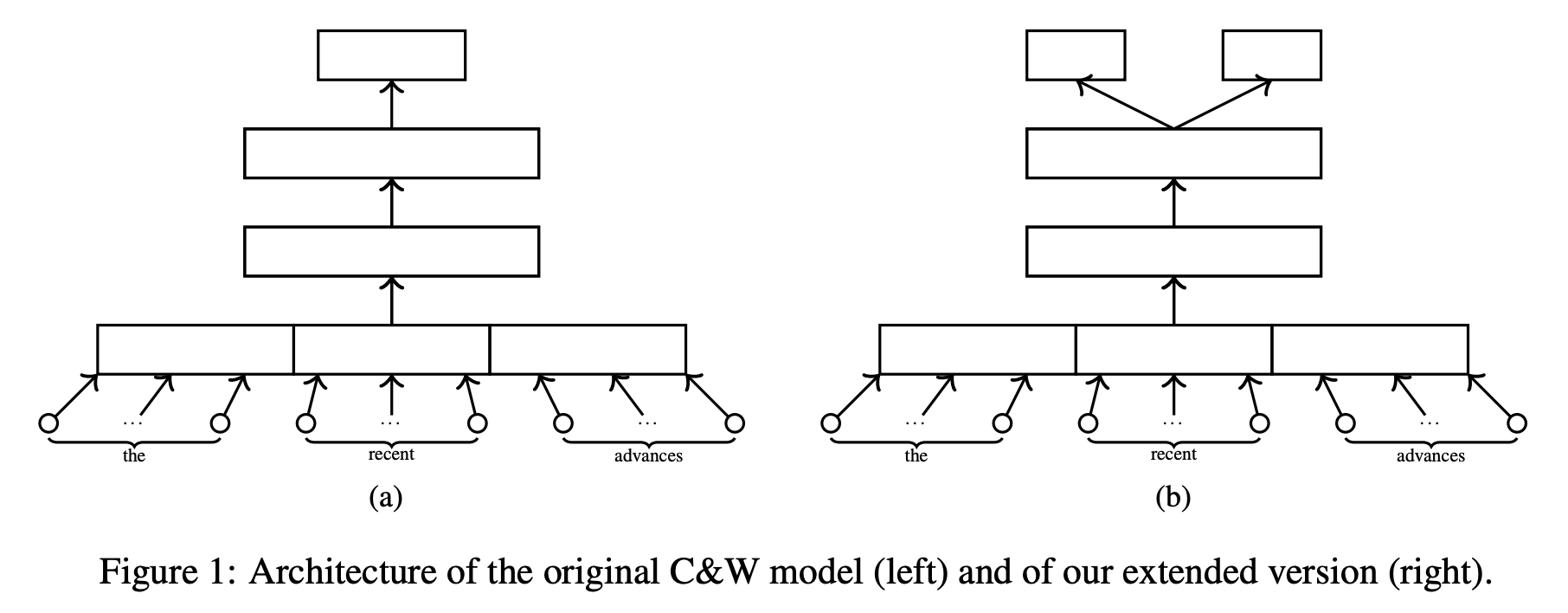
They first used a Collobert-and-Weston type architecture to pretrain word embedding with score prediction as an auxiliary task (see the figure above), in addition to the contrastive objective that captures the word's context. The idea is that, by using score prediction as an auxiliary task, the model learns in such a way that the word embeddings (called score-specific word embeddings, or SSWEs) capture useful information for predicting the score, such as misspellings.
In the next step, the learned word embeddings are fed to a biLSTM. The concatenated fist and last hidden states are fed to a linear layer and used for prediction.
Similar to Taghipour and Ng above, they tested their model on the ASAP dataset. The proposed model achieved extremely good correlation ($r = 0.96$ and $\kappa = 0.96$). One caveat is that the ASAP dataset contains several problem sets with vastly different score ranges (including both 4-point and 60-point rubrics) and the authors seem to have simply computed the metrics without any normalization, possibly overestimating the degree of correlation.

One nice thing about this work is they visualized a saliency map where words in a given essay are colored according to their "quality." In order to obtain this visualization, they feed a maximum possible score and a minimal score to the network as gold labels and computed the gradient wrt word embeddings. This corresponds to how much word embeddings need to change in order to achieve the maximum (or minimum) score. An example is shown in the figure above.
In another concurrent work, Dong and Zhang (2016) explore a full CNN architecture, where the input word embeddings are transformed through a series of alternating convolutional and pooling layers. After the final pooling layer, the activations go through a fully connected layer, which produces the predicted score directly.
A year later, the same authors (Dong et al. 2017) extended their model with a sentence-based LSTM and an attention mechanism to capture long-range dependency and the contribution of individual sentences to the final score. The attention layer computes a weighted sum of sentence hidden states instead of taking the mean over time uniformly.
BERT-based Models
To date, there are no best practices on fine-tuning Transformers for AES
The quote above (from Mayfield and Black 2020) sums it all up pretty well—in AES, there's no agreed upon set of best practices when it comes to fine-tuning pretrained models such as BERT. In the latter half of this post I'll introduce three papers that do this, with varying degrees of success.
My favorite "post-BERT" AES paper is Nadeem et al. (2019), where they explored different combinations of network architectures, contextualized embeddings, and pretraining strategies.
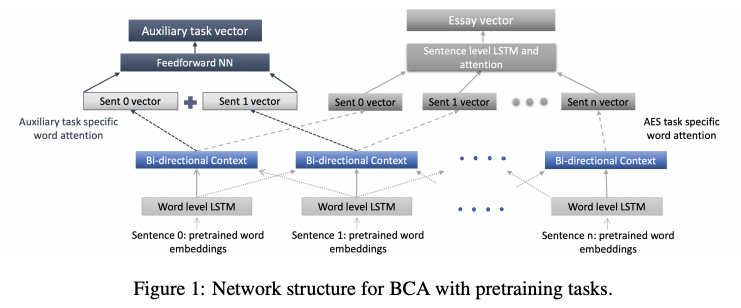
Specifically, they experimented with two LSTM-based architectures, HAN (Yang et al. 2016) and BCA (Nadeem and Ostendorf 2018), with and without BERT. They also explored two auxiliary pretraining tasks, one with natural language inference (NLI) and the other with discourse marker prediction (DM). By pretraining the model with a task that captures the discourse structures, the model can better capture the coherency of the given essay.
They found that the combination of BERT + BCA outperformed the baselines with a statistically significant margin on a larger dataset (the ETS Corpus of Non-Native Written English, which are TOEFL essays), while the use of contextualized embeddings (BERT) was not effective when the training data is small (the ASAP dataset).
They show (with nice visualization) that high scoring essays show better inter-sentence similarity structures and they hypothesize that contextual embeddings learned by BERT can better capture such structures.
In a paper titled "Should You Fine-Tune BERT for Automated Essay Scoring?" from BEA 2020, Mayfield and Black discuss trade-offs between traditional and BERT-based models for AES. Their main claim is that state-of-the-art techniques do match existing best results, while incurring significant computational cost.
Specifically, they found that BERT-based models are no better than traditional methods, while being computationally expensive and requiring intensive optimization efforts. They also identify three areas where BERT is promising for AES: domain transfer, style and voice, and fairness.
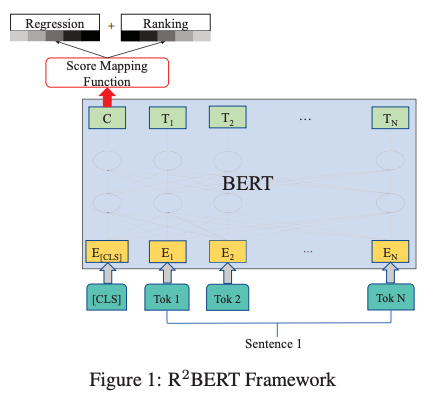
Most recently, Yang et al. 2020 (published on EMNLP 2020 Findings) showed that combining multiple objectives is effective for fine-tuning BERT for AES.
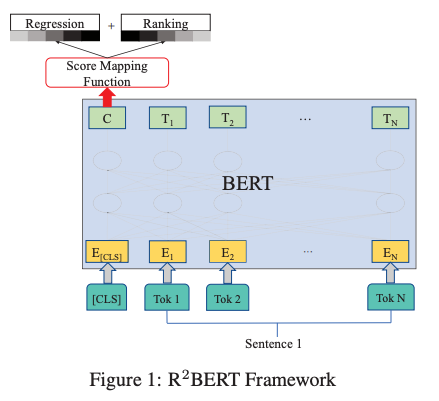
Specifically, after transforming the input with BERT, the embeddings at the CLS token were fed to a linear layer, which is then optimized with two different loss functions—one for regression and another for listwise ranking similar to ListNet, where the probability of an essay being ranked at the first position is defined by a softmax function. These two losses are linearly interpolated, while the weight for regression loss is gradually increased during the training.
In the experiments, their regression-only variant (with BERT) already outperforms other neural models, while the combination of the two losses achieves the best QWK metric.
It is important to note that by default BERT can only deal with sequences of up to 512 tokens, while many essays in the ASAP dataset are longer than this limit. The authors compared two conditions where they took the first or last 512 tokens of each essay before feeding it to BERT, which didn't show much difference. Fully utilizing information in long essays is future work.
Summary
We've seen some mixed results in applying to BERT to the problem of AES. Although we are starting to see some promising results like Yang et al. 2020, I think as of this writing, practitioners should be ready to experiment with a wide variety of methods—traditional and neural architectures, different feature representations, and training objectives, to find the combination that works best for their own task and data.